A Zero-Knowledge Proof: Improving Privacy on a Blockchain

Cryptography is one of the the most important components of the blockchain technology, which has become widely spread over the last few years. Here, we talk about a zero-knowledge proof (ZKP)—a mechanism/protocol that has a close connection to cryptography. You will learn about the general concepts of a ZKP and noninteractive zero-knowledge proof, see some use cases for employing the protocol within a blockchain, and get a dive into a ZKP from the perspective of cryptography.

What’s a zero-knowledge proof?

A zero-knowledge proof is one of the most abstract and fascinating concepts in applied cryptography today. From potentially being used in nuclear disarmament to providing anonymous and secure transactions for public blockchain networks, a zero-knowledge proof is a profound example of cryptographic innovation.

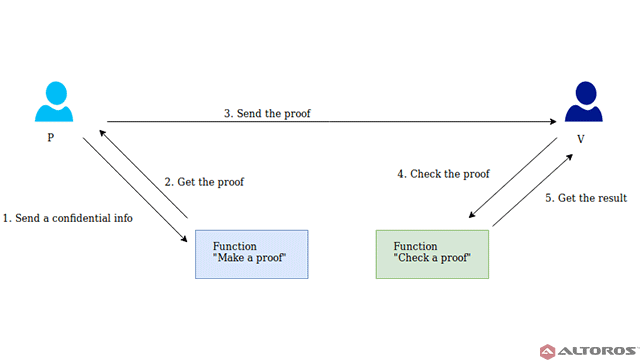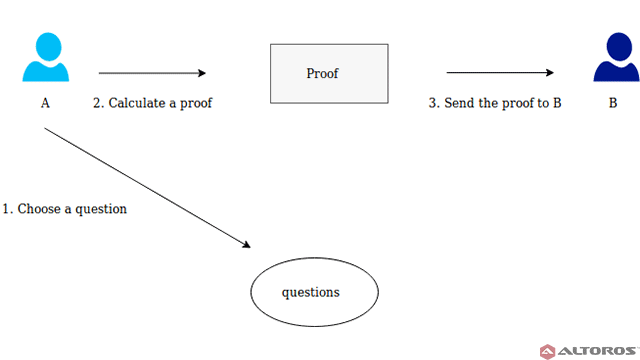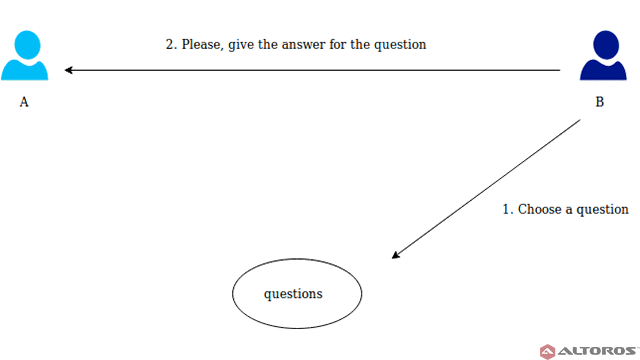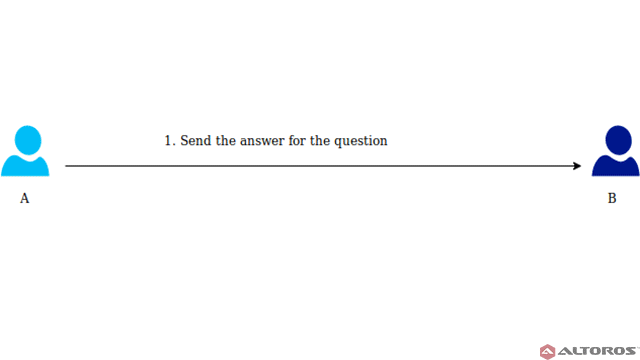
In cryptography, a zero-knowledge proof or zero-knowledge protocol is a method by which one party (the prover) can prove to another party (the verifier) that they know a value x, without conveying any information apart from the fact that they know the value x. The essence of a zero-knowledge proof is that it is trivial to prove that someone possesses knowledge of certain information by simply revealing it. The challenge is to justify such possession without revealing the information itself or any additional information.

A zero-knowledge proof must satisfy the following three parameters:

• Completeness. If the statement is true, the honest verifier—the one that is following the protocol properly—will be convinced of this fact by an honest prover.
• Soundness. If the statement is false, no cheating prover can convince the honest verifier that it is true, except for some small probability.
• Zero knowledge. If the statement is true, no verifier learns anything, except the fact that the statement is true. In other words, just knowing the statement (not the secret) is sufficient to imagine a scenario, showing that the prover knows the secret. This is achieved through each verifier having a simulator, which can produce a transcript that “looks like” an interaction between the honest prover and the verifier. The simulator should be able to produce the transcript, while only having access to the statement to be proved and not the prover itself.

Completeness and soundness are properties of more general interactive proof systems. The addition of zero knowledge is what turns the verification process into a zero-knowledge proof.

Zero-knowledge proofs are not proofs in the mathematical sense of the term, because there is some small probability, the soundness error, that a cheating prover will be able to convince the verifier of a false statement. In other words, zero-knowledge proofs are probabilistic proofs rather than deterministic ones. However, there are some techniques to decrease the soundness error to negligibly small values.

The general structure of a ZKP

The general structure of a zero-knowledge proof consists of three sequential actions between participants A and B. These actions are called a witness, a challenge, and a response.

Witness. The fact that A knows the secret determines some set of the questions, which always can be answered by A correctly. At first, A chooses randomly any question from the set and calculates a proof. Then, A sends the proof to B.

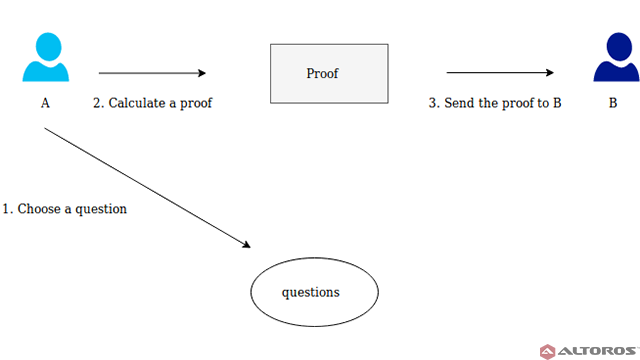A picks a random question and sends the proof to B

Challenge. After that, B chooses a question from the set and asks A to answer it.

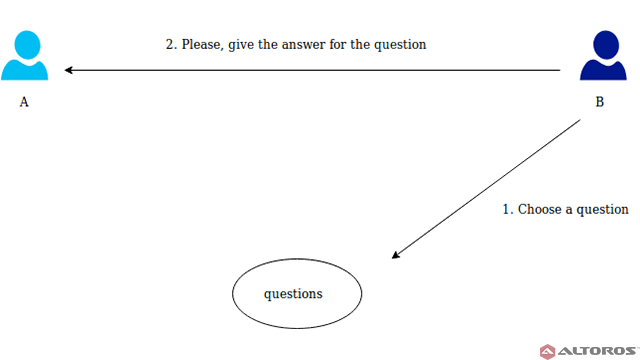B picks a random question and asks A to answer

Response. A calculates the answer and sends it back to B.

A calculates the answer and sends it to B

The received answer allows B to check that A really knows the secret.

The procedure can be repeated as many times as you want, until the probability that A makes guesses rather than knows the correct answers becomes low enough.

To illustrate how ZKP works in practice, Wikipedia refers to the Ali Baba cave story, which was first published by Jean-Jacques Quisquater. In this example, Peggy acts as the prover and Victor acts as the verifier.

In the story, the cave is shaped like a ring. The entrance is on the left side, and there’s a magic door blocking the right side. Peggy wants to prove to Victor that she knows the secret word to open the magic door. However, she does not want to reveal the secret word.

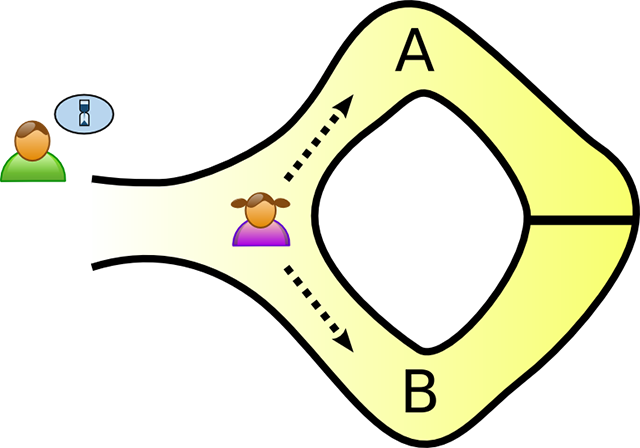Victor waits outside while Peggy picks a path (Image credit)

To prove that Peggy knows the secret word, they mark the left and right paths from the entrance as A and B. Victor waits outside the cave, while Peggy enters. Hidden from Victor, Peggy walks along either path A or B. Victor then enters the cave and shouts the name of the path—A or B—he wants Peggy to return to. Given that Peggy actually knows the secret, she can easily open the magic door, if needed, and return to the entrance using the path Victor chose.

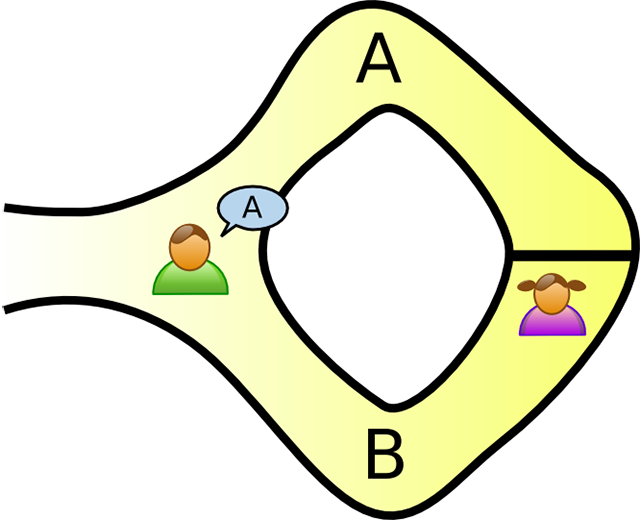Victor enters the cave and calls out a path at random (Image credit)

In case Peggy does now know the secret word, she would only be able to return from the door to the entrance if Victor called out the path she took after entering. Since the path Victor chooses in random, the probability that Peggy doesn’t know the keyword is 1/2. If you repeat the process k times, then the probability becomes (½)^k. This way, it’s enough, for example, to repeat the procedure 20 times to prove that Peggy know the keyword.

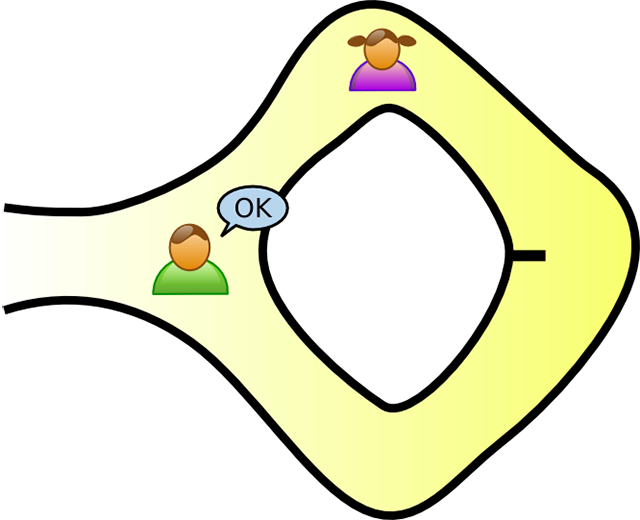Peggy returns to the entrance using the path Victor called out (Image credit)

If Victor records everything on camera, the resulting video will not be the evidence for any other party, because they could agree in advance where Peggy would go. It means that she can find the right way out without knowing the keyword itself.

As we can see, the cave example satisfies the following properties: completeness, soundness, and zero knowledge.

Note that the interaction between the users is needed for a ZKP. Although the number of interactions is small in single-round and constant protocols, both users must be involved simultaneously.

A noninteractive ZKP

Consider a situation, where users P and V are mathematicians, and they employ regular (snail) mail to communicate with each other. Mathematician P wants to travel the world and prove new theorems to mathematician V without disclosing the essence of the proof. In this scenario, we need to come up with some noninteractive protocol, since mathematician P may not have a fixed address and may move before receiving the next answer.

Blum, Feldman, and Micali suggested a noninteractive ZKP, where users P and V have a shared secret key, which is enough to prove that P knows some secret information without revealing the information itself.

Unlike a regular zero-knowledge proof, a general structure of a noninteractive ZKP consists of just a single action between participants P and V, and this action is a witness.

P passes the secret information as an argument to a special function—“make a proof” (see the image below). The output is some value of “proof.” After that, P sends “proof” to user V. Then, V can check if P knows the secret information using the “proof” and another special function—“check a proof.”

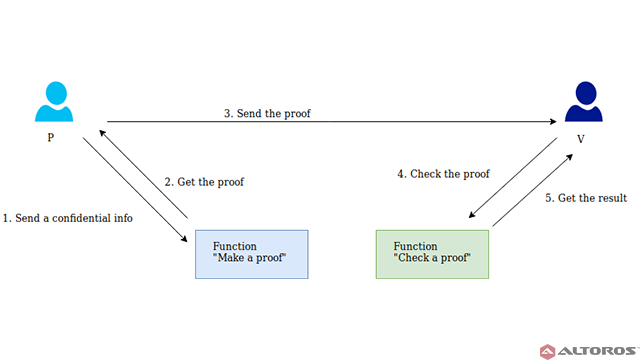In a noninteractive ZKP, A and B interact only once

Where can ZKP be applied?

Authentication systems. Research in ZKP proofs has been motivated by authentication systems, where one party wants to prove its identity to a second party via some secret information, such as a password, but doesn’t want the second party to learn anything about the secret.

Ethical behavior. One of the use cases for ZKP within cryptographic protocols is to enforce honest behavior, while maintaining privacy. Roughly, the idea is to force a user to prove, using ZKP, that its behavior is appropriate according to the protocol. Thanks to soundness, we know that a user must act honestly in order to be able to provide a valid proof. Thanks to zero knowledge, we know that a user doesn’t compromise the privacy of his/her secrets in the process of providing the proof.

Confidentiality. Another use case for ZKP is in transactions requiring confidentiality. Consider a simple public blockchain (such as Ethereum), which is tied to some cryptocurrency or a token. When the usual transaction occurs between users, blockchain records a detailed transfer information: who, to whom, and how much. Thus, if you know the specific transaction address or user address, you can make some financial conclusions. It’s essential for present-day businesses to leave some details hidden for certain transactions. In this case, a ZKP makes it possible to hide transaction details and recognize them as valid for adding to a new block. (An example of such a blockchain is Zcash.)

Checking personal information. If you want to take a loan from a bank, it’s necessary to provide an income certificate. This certificate contains confidential information. In this case, some of your personal data will be available to others, and that is what we would like to avoid. It should be enough for a bank to know a person earns a certain minimum that is required to repay a loan.

We can implement a distributed system where each user will have a special cryptographic digital identifier that contains some personal data. This digital identifier will be impossible to forge or change without its owner’s knowing. Banks and other bodies will have their own digital documents, as well.

In this system, in order to get a loan, you can take a corresponding digital income certificate from your company, the legality of which is cryptographically easy to check. You can then request a loan. The bank may then verify that you earn a required minimum using ZKP, and it’s not necessary to reveal sensitive specifics. An example of such a blockchain is Hyperledger Indy.

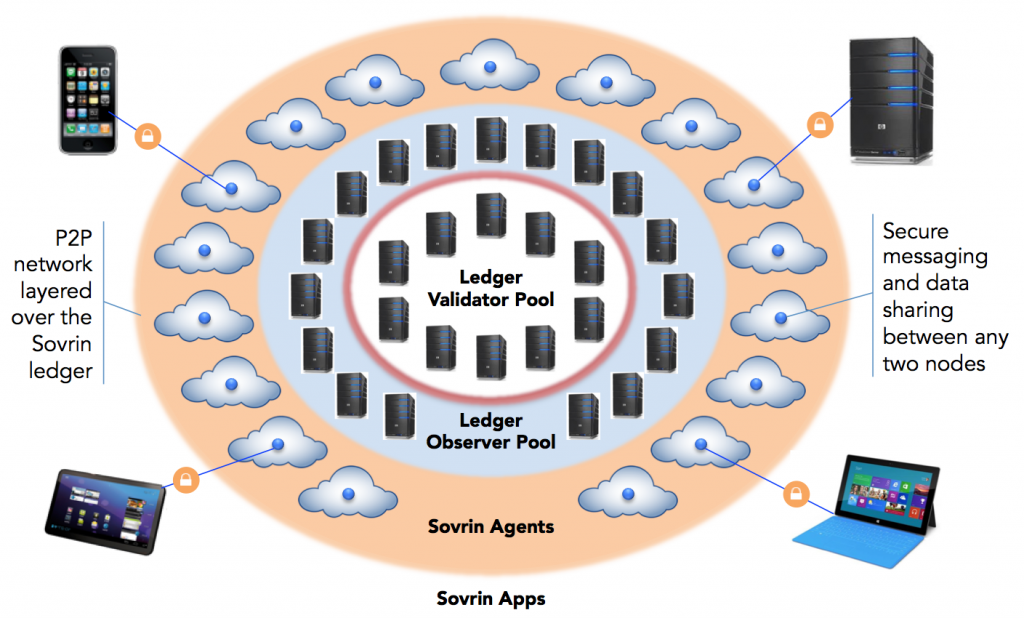Indy’s peer-to-peer off-ledger agent interaction (Image credit)

Anonymity. Sometimes, it’s necessary to have some anonymity on a blockchain. For example, making transactions without your identity being disclosed or transactions that are not connected. It should also be possible for a user to make several transactions, while keeping the identity a secret.

For these purposes, you can use Hyperledger Fabric, starting with version 1.2, which supports a special ZKP-based cryptographic protocol—Identity Mixer (Idemix).

A ZKP is a powerful cryptographic method, and its use in blockchain appears to be promising in cases where existing blockchain technologies can adapt a ZKP to address specific business requirements focusing on data privacy. For more details on the concepts behind zero-knowledge proof and its implementations, read our post on noninteractive ZKP or check out the full research paper.

Want details? Watch the video!

During a blockchain meetup in Berlin, Dmitry Lavrenov of Altoros explained the concepts surrounding ZKP in more detail.

Related slides

Further reading

• Zero-Knowledge Proof: Verifying Blockchain Transactions with Less Risk
• Securing a Blockchain with a Noninteractive Zero-Knowledge Proof
• Making Blockchain Comply with GDPR: The Challenges and Fixes
• Blockchain for Insurance: Less Fraud, Faster Claims, and New Models

About the author

Dmitry Lavrenov is Senior Blockchain R&D Engineer at Altoros. With a profound expertise in cryptography, he is knowledgeable about encryption algorithms, cryptanalysis, hash functions, and digital signatures. Dmitry is experienced in developing solutions based on Ethereum, EOS.IO, and Hyperledger Fabric for FinTech, healthcare, and other industries. He also possesses practical skills in synthesis and cryptanalysis of block and stream encryption algorithms, as well as in reverse engineering, analysis of software implementations, and malware analysis.

This blog post was written by Dmitry Lavrenov
with assistance from Carlo Gutierrez, Sophia Turol, and Alex Khizhniak.