Building Recommenders with Multilayer Perceptron Using TensorFlow

The accuracy of recommendations

Oliver Gindele

Recommenders are widely used by e-commerce and multimedia companies worldwide to provide relevant items to a user. Many different algorithms and models exist to tackle the problem of finding the best product in retail, telco, and other industries. Recently, we have written how Google created a solution to enable real-time recommendations of TV shows based on little data available.

Within TensorFlow, there is a bunch of in-built high-level APIs that help to improve the accuracy of recommendation engines. At a TensorFlow meetup in London, Oliver Gindele of Datatonic expanded on the topic. He examplified popular recommendation systems like Netflix and the ones some don’t even think as of a recommender in the first place.

For instance, Google Search, which provides highly personalized suggestions whenever a user types in the input. The accuracy of recommendations is of critical importance for end-user experience. Oliver backed up his idea by illustrating that when he looked for “python” on Google, it returned the results for the Python programming language rather than a snake. In addition, Google will offer to check out similar solutions that a user may not have interacted with previously, but the system decides they may be of interest.

During his session, Oliver explained how to optimize such common recommendation models as collaborative filtering and multilayer perceptron using TensorFlow.

Collaborative filtering

So, what makes recommendation engines recommend? One of the common techniques is to build a matrix, demonstrating how users interact with a number of items, let’s say, books. Users rate books on a scale from one to five. The matrix may be quite sparse, either because not every user has read each of the books or just won’t give any rating. This poses a problem as you need the matrix with no empty fields to make a precise recommendation.

Collaborative filtering helps to resolve this issue by breaking the matrix into two smaller matrices: a user-centric one and an item-centric one. Then, these two are compressed into a latent space to get detached latent representations of both the users and items. To get the necessary rating, one multiplies a user row with an item row.

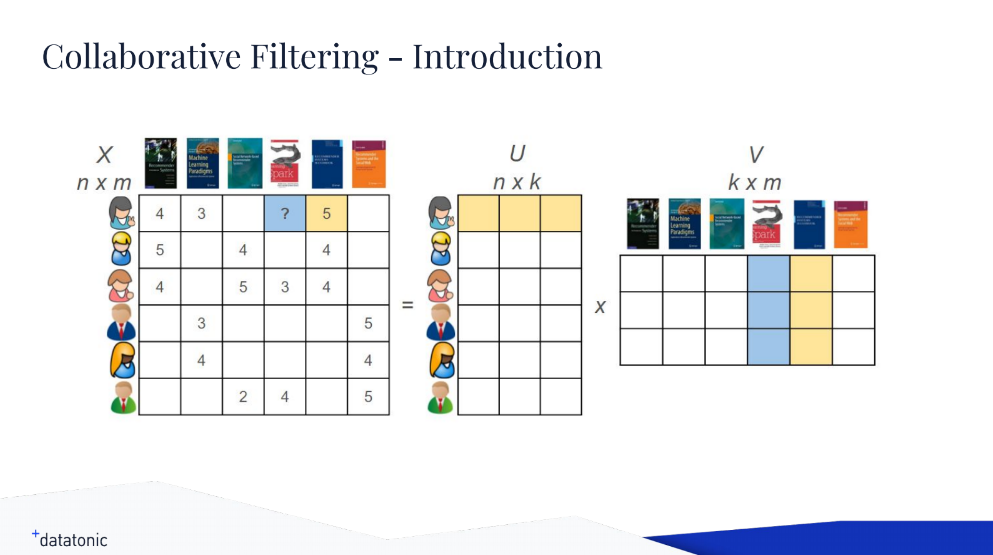A schematic visualization of collaborative filtering (Image credit)

The approach gained its popularity back in 2009, when Netflix held an open competition for the best collaborative filtering algorithm to predict user ratings for movies. According to Oliver, the winning solution was based on singular-value decomposition, the alternating least squares method, and stochastic gradient descent.

However, there are other models underlying recommenders, such as k-means clustering, matrix factorization, multilayer perceptron, etc.

Automating matrix factorization with TensorFlow

To demonstrate how the same can be done with TensorFlow in a faster manner, Oliver chose to showcase the working mechanics on a dating system. For the purpose, he utilized the LibimSeTi data set available online with:

• 17,359,346 ratings on a scale from one to ten
• 135,359 users (69% female and 31% male)
• Mean rating of 5.9

To train the model, Oliver relied on TensorFlow’s Dataset API (tf.data) and Estimators API (tf.estimator).

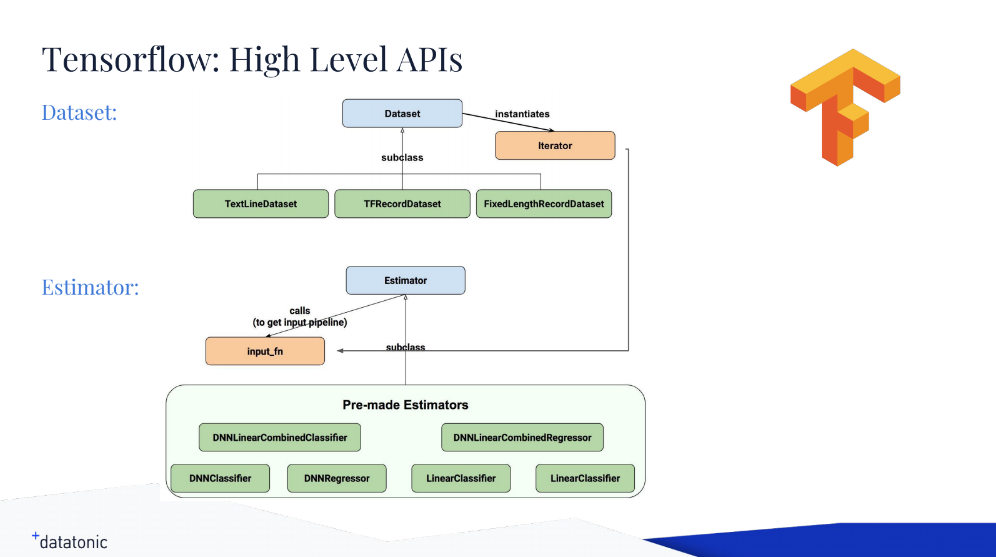High-level architectures of the Dataset and Estimators APIs (Image credit)

With tf.data, Oliver first fetched the data by defining the import function.

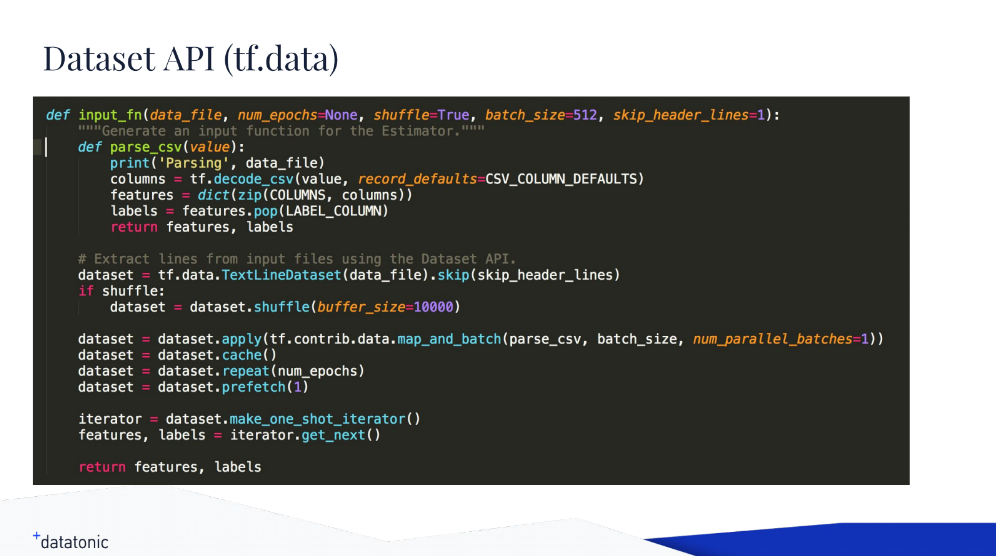Using the Dataset API to import data (Image credit)

“The nice thing here is that it’s really optimized. It uses C++ queues under the hood, and you don’t have to tweak or tune it in any way.” —Oliver Gindele, Datatonic

Oliver demonstrated a code sample of optimizing the loss function with tf.estimator.

Using the estimators API to tune the loss function (Image credit)

One needs to translate input data into representations that TensorFlow can handle. Here, tf.feature_column may be of help, serving as intermediary between raw data and Estimators. Applying embedding columns, it is possible to compress categorical columns into a dense vector of a smaller dimension. “And this is what matrix factorization approach is about,” noted Oliver.

Matrix factorization with TensorFlow (Image credit)

Now, we’ve got latent space representation of the users and the items that can be mapped to a TensorFlow model. To reproduce ratings, one calculates the dot product, adds some biases and regularization if needed, and calculates the mean squared errors. This is the equivalent of singular-value decomposition—though, done with TensorFlow in a more optimized way.

Utilizing the same embeddings, one can build a multilayer perceptron on top and train on that, running matrix factorization in parallel. In contrast to matrix factorization, the multilayer perceptron allows for easily adding any available metadata—gender or age, for instance.

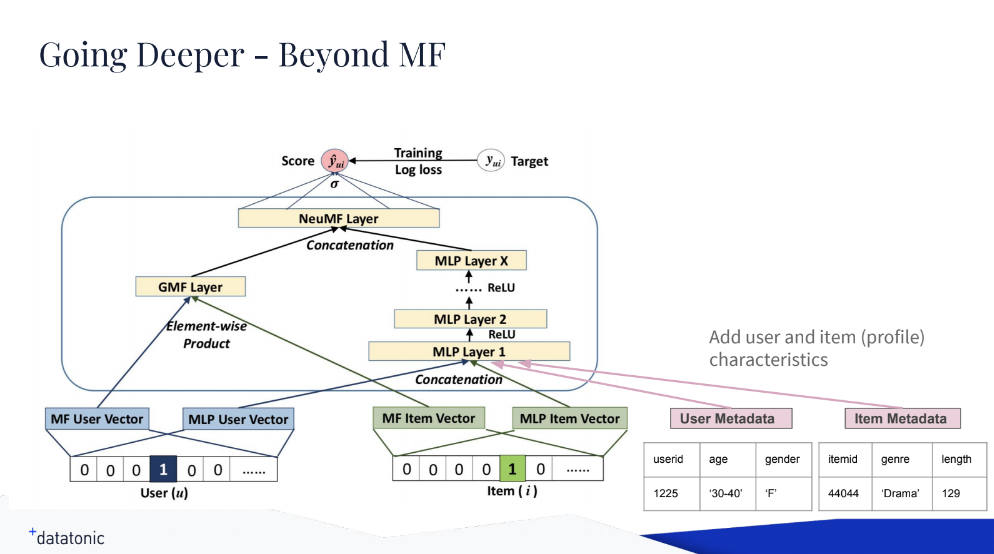Multilayer perceptron with TensorFlow (Image credit)

“A bit of a shortcoming of the matrix factorization approach is that we only put in a user ID and an item ID. If you have any metadata, let’s say, on the customers we have or the items we serve, this gets lost, and we need to find a more complex way to reintroduce it into a model. In TensorFlow, we can flexibly write our layers and model the architecture as we want. This is not an issue anymore.” —Oliver Gindele, Datatonic

Oliver has reached the following results while training the model, exploiting the matrix factorization and multilayer perceptron approaches individually. Root-mean-square error amounted to 2.137 with matrix factorization against 2.112 with multilayer perceptron. Mean absolute error amounted to 1.552 with matrix factorization against 1.541 with multilayer perceptron. Combining the two approaches allowed for minimizing root-mean-square error down to 2.071 and mean absolute error to 1.432.

Improving recommendations even further

Oliver then enumerated a few approaches and techniques that enable further improvements in building recommendation systems. For instance, delivering highly personalized recommendations based on prior implicit feedback (e.g., video length or clicks) rather than rare explicit ratings, which users aren’t always willing to submit. Logistic matrix factorization is another way of treating implicit feedback suggested by Christopher C. Johnson of Spotify. Oliver also mentioned negative sampling, which poses an alternative to the hierarchical softmax, as well as using such ranking metrics as Hit Rate (HitRate@K) for better evaluation.

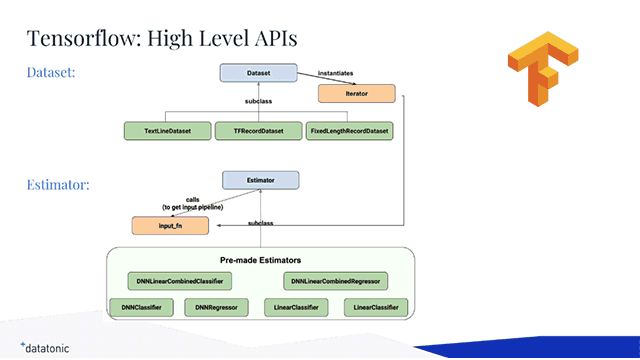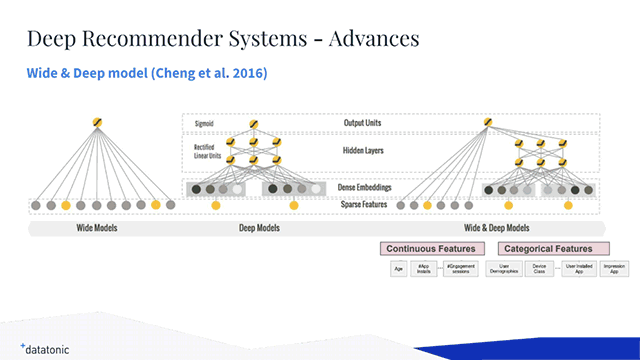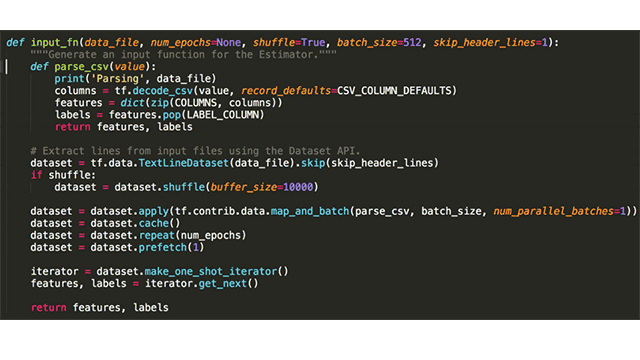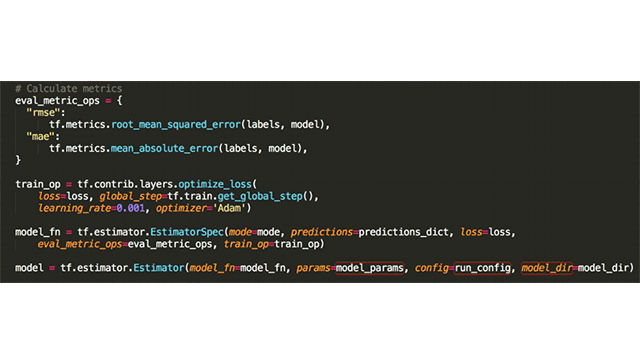
In addition, he referred to Google’s Wide & Deep learning approach, which suggests training wide linear models and deep neural networks together to join forces of both memorization and generalization for recommendation engines. This very technique was tested on a commercial mobile app store with over a billion active users and over a million apps, and its implementation is open-sourced in TensorFlow.

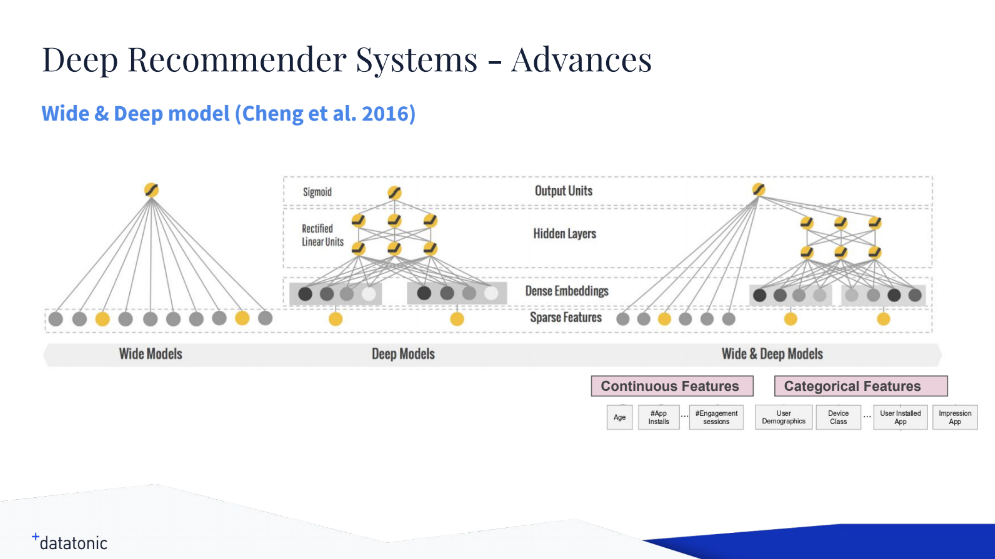A high-level architecture of the Wide & Deep learning model (Image credit)

Another Google’s advance to turn to, according to Oliver, is deep neural networks for YouTube recommendations—a driving force behind one of the most sophisticated recommenders.

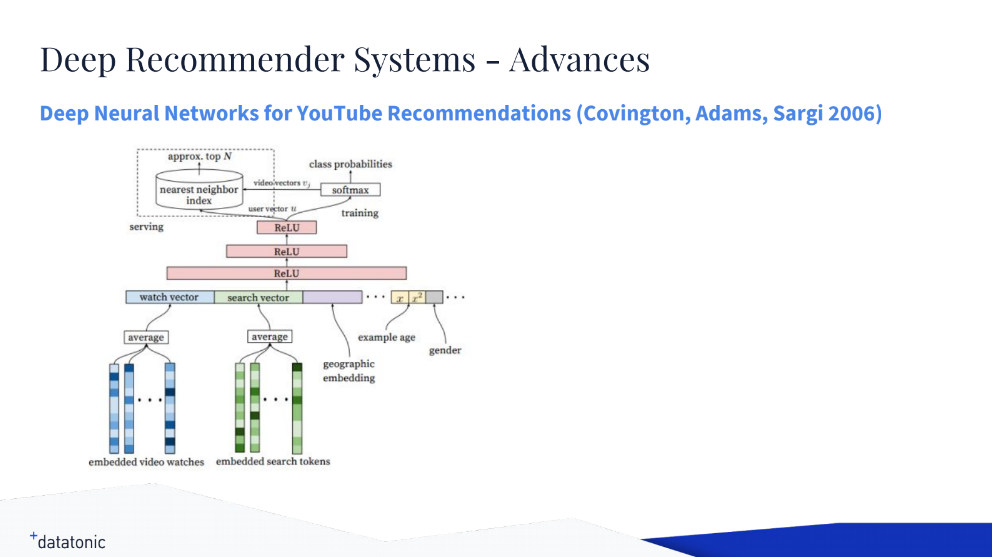A high-level architecture of deep neural networks for YouTube recommendations (Image credit)

To sum it up, Oliver highlighted that using TensorFlow helps to significantly enhance the processes of deploying, training, and scaling a model, as well as allows for implementing custom algorithms quite straightforwardly.

Want details? Watch the video!

Related slides

Further reading

• TensorFlow for Recommendation Engines and Customer Feedback Analysis
• Machine Learning for Automating a Customer Service: Chatbots and Neural Networks
• The Diversity of TensorFlow: Wrappers, GPUs, Generative Adversarial Networks, etc.

About the expert

Oliver Gindele is a Data Scientist at Datatonic. With a background in computational physics and high-performance computing, he is a machine learning practitioner experimenting with different deep learning solutions. Oliver holds a MSc degree in Material Science from ETH Zürich and a PhD degree in Physics from University College London.